
“In particular, formula 5 (and 6) as presented here, totally rules out any possibility that a 33°C greenhouse effect of the type proposed by the IPCC in their reports can exist in the real atmosphere.” – Holmes, 2017
In a new peer-reviewed scientific paper published in the journal Earth Sciences last December (2017), a Federation University (Australia) Science and Engineering student named Robert Holmes contends he may have found the key to unlocking our understanding of how planets with thick atmospheres (like Earth) remain “fixed” at 288 Kelvin (K), 740 K (Venus), 165 K (Jupiter)…without considering the need for a planetary greenhouse effect or changes in atmospheric CO2 concentrations.
The Greenhouse Effect ‘Thought Experiment’
Perhaps the most fundamental conceptualization in climate science is the “thought experiment” that envisions what the temperature of the Earth might possibly be if there was no greenhouse effect, greenhouse gases, or atmosphere.
Dr. Gavin Schmidt, NASA
“The size of the greenhouse effect is often estimated as being the difference between the actual global surface temperature and the temperature the planet would be without any atmospheric absorption, but with exactly the same planetary albedo, around 33°C. This is more of a ‘thought experiment’ than an observable state, but it is a useful baseline.”
Simplistically, the globally averaged surface temperature clocks in at 288 K. In the “thought experiment”, an imaginary Earth that has no atmosphere (and thus no greenhouse gases to absorb and re-emit the surface heat) would have a temperature of only 255 K. The difference between the real and imagined Earth with no atmosphere is 33 K, meaning that the Earth would be much colder (and uninhabitable) without the presence of greenhouse gases bridging the hypothetical “heat gap”.
Of that 33 K greenhouse effect, 20.6 K is imagined to derive from water vapor droplets in the atmosphere (1,000 to 40,000 parts per million [ppm] by volume), whereas 7.2 K is thought to stem from the “natural” (or pre-industrial) 200-280 ppm atmospheric CO2 concentration (Kramm et al., 2017).
As a “thought experiment”, the critical heating role for water vapor droplets and CO2 concentrations lacks real-world validation. For example, the Earth’s oceans account for 93% of the planet’s heat energy (Levitus et al., 2012), and yet no real-world physical measurements exist that demonstrate how much heating or cooling is derived from varying CO2 concentrations up or down over a body of water in volume increments of parts per million (0.000001). Consequently, the CO2 greenhouse effect is a hypothetical, model-based conceptualization.
And in recent years, many scientific papers have been published that question the fundamentals of not only the Earth’s hypothetical greenhouse effect, but the role of greenhouse gases for other planets with thick atmospheres (like Venus) as well Hertzberg et al., 2017, Kramm et al., 2017, Nikolov and Zeller, 2017 , Allmendinger, 2017, Lightfoot and Mamer, 2017, Blaauw, 2017, Davis et al., 2018). The Holmes paper highlighted here may just be among the most recent.
‘Extremely Accurate’ Planetary Temperature Calculations With Pressure/Density/Mass Formula
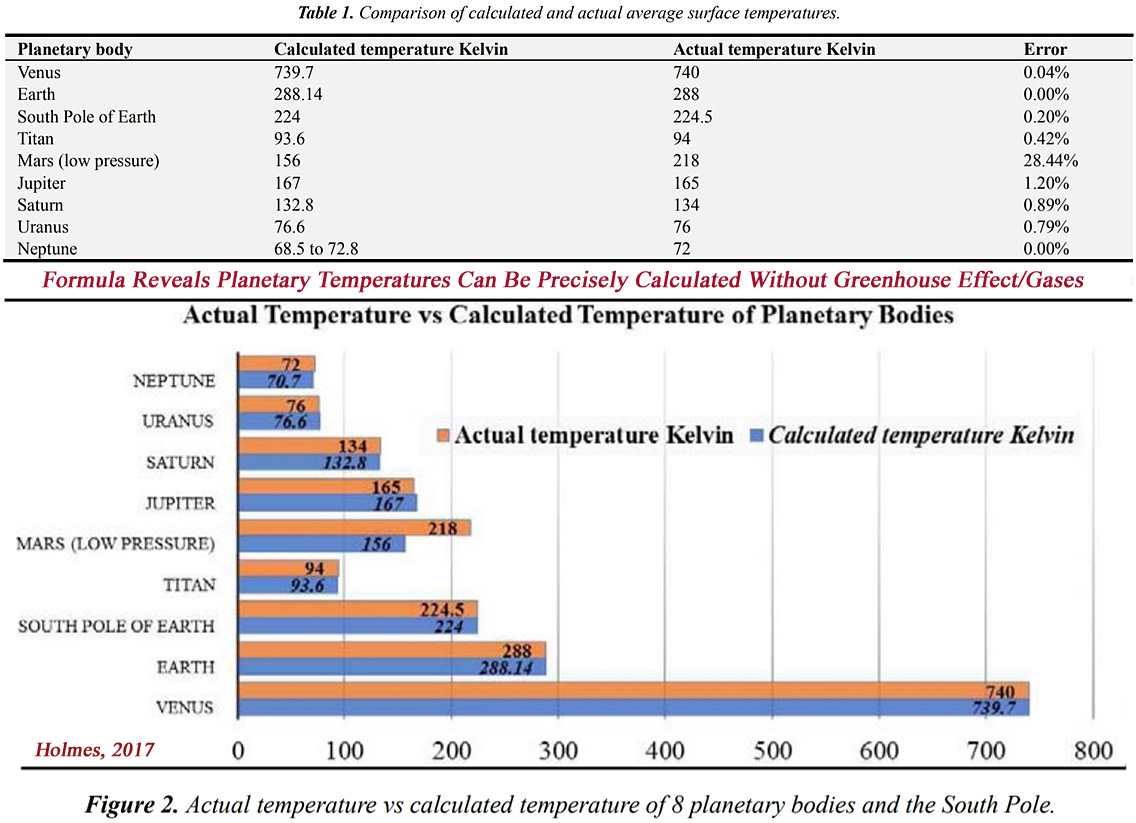
Holmes has argued that the average temperature for 8 planetary bodies with thick (0.1 bar or more) atmospheres can be precisely measured with “extreme” accuracy — an error range of just 1.2% — by using a formula predicated on the knowledge of 3 parameters: “[1] the average near-surface atmospheric pressure, [2] the average near surface atmospheric density and [3] the average mean molar mass of the near-surface atmosphere.”
Holmes used the derived pressure/density/mass numbers for each planetary body. He then calculated the planets’ temperatures with these figures.
Venus’ temperature was calculated to be 739.7 K with the formula. Its measured temperature is 740 K. This indicates that the formula’s accuracy is within an error range of just 0.04% for Venus.
Given Earth’s pressure/density/mass, its calculated temperature is 288.14 K using Holmes’ formula. Earth’s measured temperature is 288 K, an exact fit.
Saturn’s calculated temperature is 132.8 K. Its measured temperature is 134 K — an error range of only 0.89%.
The impressive accuracy of the formula is illustrated below in Table 1. and Figure 2.
Atmospheric Pressure/Density And Surface Temperature
In large part, the density of a planet’s atmosphere is a primary determinant of its temperature. Planets with thick atmospheres are hotter. Planets with thin atmospheres are cooler. The further away from the surface, the less gravity/pressure there is and the cooler it gets. And vice versa.
Sciencing.com
“In general, the weaker the gravitational pull of a planet, the thinner the atmosphere will be. A planet with weak gravity will tend to have less mass and allow more atmosphere to escape into space. Thus the thickness or thinness of the atmosphere depends upon the strength or weakness of gravity. For example, the gravity on Jupiter is 318 times greater than Earth, and thus Jupiter’s atmosphere is much thicker than Earth’s. Gravity gets weaker the further away it is from a planet, so the atmosphere will be thicker near the surface.”
A facile illustration of the effects of atmospheric pressure on the surface temperatures of a planet like Earth can be found in the Grand Canyon, Southwestern U.S. There, the North Rim is about 1,000 feet (305 meters) higher in elevation than the South Rim. Interestingly, the North Rim is also about 9 degrees Fahrenheit colder than the South Rim due to the influence of atmospheric pressure/gravity. The bottom of the canyon reaches temperatures 20-25 degrees warmer than the top. The stark temperature difference is unrelated to the greenhouse gas concentrations for the two locations, nor is it connected to sunlight. It’s the gravitational pressure that creates the heat divergence.
Subia, 2014
“Elevation and season of the year determine average temperatures at the the Grand Canyon. Elevations at top of the South Rim average around 7,000 feet. The North Rim averages about 8,000 feet. The higher the elevation, the cooler the temperature. At any given time, the North Rim will average 8-10 degrees Fahrenheit cooler versus the South Rim. … [T]he very bottom of the canyon can increase 20 to 25 degrees warmer than the top of the respective rims.”
Sensitivity To CO2 Concentration Changes ‘Extremely Low’
Holmes points out that the implications of his precise calculations for planetary temperatures necessarily lead to the conclusion that there is no need to have a greenhouse effect or greenhouse gases to bridge a hypothetical “heat gap.” Instead, he writes that “planetary bodies with thick atmospheres cannot be mainly determined by the ‘greenhouse effect’, but instead most likely by an effect from fluid dynamics, namely, adiabatic autocompression.”
This effectively rules out the possibility that CO2 is a predominant climate driver.
In fact, Holmes’ calculation for CO2 climate sensitivity (doubling the atmospheric CO2 concentration from 0.03% to 0.06%) is -0.03°C.
As he ostensibly understates in his conclusion, “This climate sensitivity is already so low that it would be impossible to detect or measure in the real atmosphere.”
Holmes, 2017
Molar Mass Version of the Ideal Gas Law
Points to a Very Low Climate Sensitivity
Introduction
Presented here is a simple and reliable method of accurately calculating the average near surface atmospheric temperature on planetary bodies which possess a surface atmospheric pressure of over 10kPa [a thick atmosphere, 0.1 bar or more]. This method requires a gas constant and the knowledge of only three gas parameters: [1] the average near-surface atmospheric pressure, [2] the average near surface atmospheric density and [3] the average mean molar mass of the near-surface atmosphere. The formula used is the molar version of the ideal gas law.
It is here demonstrated that the information contained in just these three gas parameters alone is an extremely accurate predictor of atmospheric temperatures on planets with atmospheres >10kPa. This indicates that all information on the effective plus the residual near-surface atmospheric temperature on planetary bodies with thick atmospheres, is automatically ‘baked-in’ to the three mentioned gas parameters.
This formula proves itself here to be not only more accurate than any other method heretofore used, but is far simpler to calculate. It requires no input from parameters previously thought to be essential; solar insolation, albedo, greenhouse gas content, ocean circulation and cloud cover among many others.
Given this, it is shown that no one gas has an anomalous effect on atmospheric temperatures that is significantly more than any other gas.
In short, there can be no 33°C ‘greenhouse effect’ on Earth, or any significant ‘greenhouse effect’ on any other planetary body with an atmosphere of >10kPa.
The Formula: An ‘Extremely Accurate Predictor’ Of Planetary Temperatures

[T]he hypothesis being put forward here is that in the case of Earth, solar insolation provides the ‘first’ 255 Kelvin – in accordance with the black body law [11]. Then adiabatic auto-compression provides the ‘other’ 33 Kelvin, to arrive at the known and measured average global temperature of 288 Kelvin. The ‘other’ 33 Kelvin cannot be provided by the greenhouse effect, because if it was, the molar mass version of the ideal gas law could not then work to accurately calculate planetary temperatures, as it clearly does here.
It is apparent that this simple formula calculates the ‘surface’ temperatures of many planetary bodies in our Solar System accurately (Figure 2).
Specifically, those which have atmospheres thick enough to form a troposphere (i.e. possessing an atmospheric pressure of over 10kPa or 0.1bar). These are: Venus, Earth, Jupiter, Saturn, Titan, Uranus and Neptune. All calculated temperatures are within 1.2% of the NASA reported ‘surface’ temperature (except for Mars, which is excluded because it has a much lower atmospheric pressure than 10kPa).
This accuracy is achieved without using the S-B black body law, or the need to include terms for such parameters as TSI levels, albedo, clouds, greenhouse effect or, for that matter, adiabatic auto-compression. All that is required to be able to accurately calculate the average near-surface atmospheric temperature, is the relevant gas constant and the knowledge of three variable gas parameters.
The Implications: CO2 Climate Sensitivity (-0.03°C) ‘Extremely Low’
Some reflection upon the simplicity and accuracy of these results will bring an unbiased person to the obvious implications of this work. These are that the residual (residual being the difference between S-B law results and actual) near-surface atmospheric temperatures on planetary bodies with thick atmospheres cannot be mainly determined by the ‘greenhouse effect’, but instead most likely by an effect from fluid dynamics, namely, adiabatic autocompression.
Another implication leads directly to the conclusion that the climate sensitivity to, for example, a doubling of the atmospheric carbon dioxide concentration has to be operating instantaneously, and also must be extremely low. Under this scenario, the climate sensitivity to CO2 cannot be very different to the addition of a similar quantity of any other gas.
In particular, formula 5 (and 6) as presented here, totally rules out any possibility that a 33°C greenhouse effect of the type proposed by the IPCC in their reports [23] can exist in the real atmosphere. The reason is that the IPCC state in their reports that a 0.03% [300 ppm] increase in atmospheric CO2 (i.e. a doubling from pre-industrial levels) must result in a global temperature rise of ~3°C; (a range of 1.5°C to 4.5°C, which has hardly changed since 1990) [24]. This is the so-called ‘climate sensitivity’. Anything like this magnitude of warming caused by such a small change in gas levels is completely ruled out by the molar mass version of the ideal gas law.
Calculate for a doubling of CO2 from the pre-industrial level of 0.03% [300 ppm]:
Calculated temperature after doubling of CO2 to 0.06% ≈ 288.11K. Climate sensitivity to CO2 is ≈ 288.14 – 288.11 ≈ – 0.03K.
The change would in fact be extremely small and difficult to estimate exactly, but would be of the order -0.03°C. That is, a hundred times smaller than the ‘likely’ climate sensitivity of 3°C cited in the IPCC’s reports, and also probably of the opposite sign [cooling]. Even that small number would likely be a maximum change, since if fossil fuels are burned to create the emitted CO2, then atmospheric O2 will also be consumed, reducing that gas in the atmosphere – and offsetting any temperature change generated by the extra CO2. This climate sensitivity is already so low that it would be impossible to detect or measure in the real atmosphere, even before any allowance is made for the consumption of atmospheric O2.
Ref.: http://notrickszone.com/2018/02/05/shock-paper-cites-formula-that-precisely-calculates-planetary-temps-without-greenhouse-effect-co2/#sthash.g7koEldO.4nTQZ0Yb.dpbs
Comment:
This information will do nothing to the “greens” policy, it won’t change anything, all taxes planned will be put in place and forced upon people and businesses.
.. because the (Man Made) Global Warming Swindle has never been about the science, CO2., facts, logic or common sense, it has always been about money, carbon taxes, Cap’n Trade and tax on energy.
Politics and reason has always been a bad match!


